Categorical Encoding Demystified

machine-learning
encoding
Author

Krishnakanta Maity

Published

December 19, 2024

1 Introduction

In real-world datasets, not all variable is numeric. Many are categorical — for example:

  • city: {Delhi, Mumbai, Chennai}
  • education: {Graduate, Postgraduate, PhD}
  • gender: {Male, Female}

But mathematical calculation can be done in numerics only, thats why machine learning models require numbers as inputs. That’s where categorical encoding comes in.

In this blog, we’ll explore the three most common encoding techniques:

  1. One-Hot Encoding
  2. Label Encoding
  3. Target Encoding

and see how they behave in a regression task.

2 Dataset

Let’s simulate a simple dataset of house prices with a few categorical features.

Code 
import pandas as pd
import numpy as np
from sklearn.preprocessing import OneHotEncoder, LabelEncoder
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score, mean_squared_error
import matplotlib.pyplot as plt
import warnings; warnings.filterwarnings("ignore")
Code 
# Create synthetic dataset
np.random.seed(42)
sample_size = 1000
data = pd.DataFrame({
    'city': np.random.choice(['Delhi', 'Mumbai', 'Chennai', 'Kolkata'], sample_size),
    'furnishing': np.random.choice(['Furnished', 'Semi', 'Unfurnished'], sample_size),
    'size_sqft': np.random.randint(500, 2000, sample_size),
    'price_lakhs': np.random.randint(30, 120, sample_size)
})

data
city furnishing size_sqft price_lakhs
0 Chennai Semi 1295 93
1 Kolkata Unfurnished 1472 39
2 Delhi Furnished 1092 67
3 Chennai Furnished 1637 110
4 Chennai Furnished 1563 37
... ... ... ... ...
995 Delhi Semi 1784 76
996 Delhi Semi 1272 64
997 Kolkata Semi 849 48
998 Kolkata Furnished 1875 37
999 Chennai Furnished 1019 55

1000 rows × 4 columns

3 0️⃣↔︎️1️⃣ 1. One-Hot Encoding

One-Hot Encoding creates a new column for each category. Each row gets a binary (0 or 1) depending on whether the category applies.

Code 
# one-hot encode
df_ohe = data.copy()
encoder = OneHotEncoder(sparse_output=False)
encodedObj = encoder.fit_transform(df_ohe[['city']])
df_encoded = pd.DataFrame(encodedObj, columns=encoder.get_feature_names_out(['city']))
print(df_encoded.head())
# combine with original dataframe
df_ohe = pd.concat([df_ohe, df_encoded], axis=1).reset_index(drop=True)
print(df_ohe.head())
   city_Chennai  city_Delhi  city_Kolkata  city_Mumbai
0           1.0         0.0           0.0          0.0
1           0.0         0.0           1.0          0.0
2           0.0         1.0           0.0          0.0
3           1.0         0.0           0.0          0.0
4           1.0         0.0           0.0          0.0
      city   furnishing  size_sqft  price_lakhs  city_Chennai  city_Delhi  \
0  Chennai         Semi       1295           93           1.0         0.0   
1  Kolkata  Unfurnished       1472           39           0.0         0.0   
2    Delhi    Furnished       1092           67           0.0         1.0   
3  Chennai    Furnished       1637          110           1.0         0.0   
4  Chennai    Furnished       1563           37           1.0         0.0   

   city_Kolkata  city_Mumbai  
0           0.0          0.0  
1           1.0          0.0  
2           0.0          0.0  
3           0.0          0.0  
4           0.0          0.0
CautionWhen to use
  • Works best when the number of unique categories is small.
  • Avoid if the column has many unique values — it leads to the curse of dimensionality.

4 🔠↔︎️🔢 2. Label Encoding

Label Encoding simply assigns a numeric label to each category.

Code 
# label encode
df_le = data.copy()
encoder = LabelEncoder()
encodedObj = encoder.fit_transform(df_le[['city']])
# get mapper
print(dict(zip(encoder.classes_, encoder.transform(encoder.classes_))))
df_encoded = pd.DataFrame(encodedObj, columns=['city_le'])
print(df_encoded.head())
# combine with original dataframe
df_le = pd.concat([df_le, df_encoded], axis=1).reset_index(drop=True)
print(df_le.head())
{'Chennai': np.int64(0), 'Delhi': np.int64(1), 'Kolkata': np.int64(2), 'Mumbai': np.int64(3)}
   city_le
0        0
1        2
2        1
3        0
4        0
      city   furnishing  size_sqft  price_lakhs  city_le
0  Chennai         Semi       1295           93        0
1  Kolkata  Unfurnished       1472           39        2
2    Delhi    Furnished       1092           67        1
3  Chennai    Furnished       1637          110        0
4  Chennai    Furnished       1563           37        0
WarningWarning

Models may interpret the numeric labels as ordinal (i.e., ordered), even when they’re not. That can mislead linear models like regression.

CautionWhen to use
  • Works fine for tree-based models (e.g., RandomForest, XGBoost).
  • Avoid for linear regression, SVM, or distance-based models.

5 🎯↔︎️🔢 3. Target Encoding

Target Encoding replaces each category with the average value of the target variable (like price).

Code 
df_te = data.copy()
df_te['city_target'] = df_te.groupby('city')['price_lakhs'].transform('mean')
df_te[['city', 'price_lakhs', 'city_target']]
city price_lakhs city_target
0 Chennai 93 74.900862
1 Kolkata 39 75.878571
2 Delhi 67 70.445736
3 Chennai 110 74.900862
4 Chennai 37 74.900862
... ... ... ...
995 Delhi 76 70.445736
996 Delhi 64 70.445736
997 Kolkata 48 75.878571
998 Kolkata 37 75.878571
999 Chennai 55 74.900862

1000 rows × 3 columns

CautionWhen to use
  • Great for high-cardinality features (many unique categories).
  • Risk of data leakage — use it only within cross-validation folds.

6 ⚖️ Comparing Impact in a Regression Task

Let’s see how encoding affects a simple linear regression model.

6.1 One-Hot Encoding

Code 
# Use one-hot encoded data for regression
X = df_ohe.drop(columns=['city','furnishing','price_lakhs'])
print(f"Independent variable/Feature(s): {list(X.columns)}")
y = df_ohe['price_lakhs']
print(f"Dependent variable/Target: {y.name}")

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# training
model_ohe = LinearRegression()
model_ohe.fit(X_train, y_train)
# prediction
preds_ohe = model_ohe.predict(X_test)
print(pd.DataFrame({'Actual': y_test, 'Predicted': np.round(preds_ohe, 2)}).head())
# evaluation
r2_ohe = r2_score(y_test, preds_ohe)
mse_ohe = mean_squared_error(y_test, preds_ohe)
print(f"""R² Score: {r2_ohe:0.6f}, MSE: {mse_ohe:0.6f}""")
Independent variable/Feature(s): ['size_sqft', 'city_Chennai', 'city_Delhi', 'city_Kolkata', 'city_Mumbai']
Dependent variable/Target: price_lakhs
     Actual  Predicted
521     108      75.04
737      48      70.66
740     113      75.08
660     112      76.98
411      69      77.28
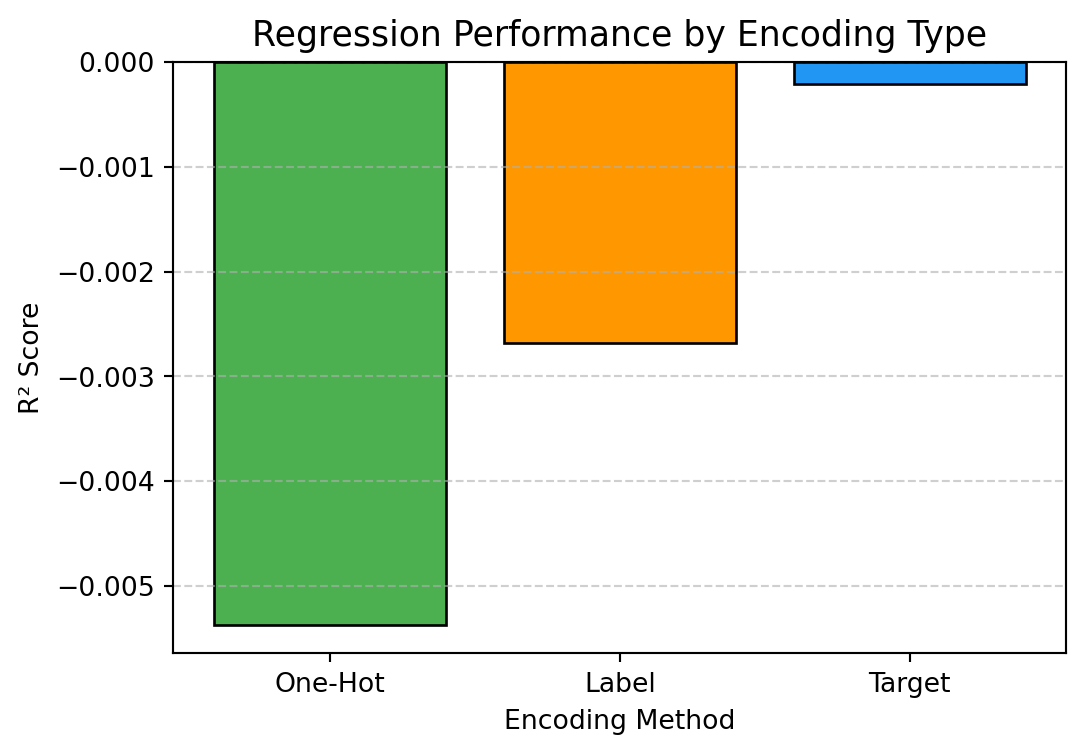
R² Score: -0.005375, MSE: 673.276323

6.2 Label Enconding

Code 
X = df_le.drop(columns=['city','furnishing','price_lakhs'])
print(f"Independent variable/Feature(s): {list(X.columns)}")
y = df_le['price_lakhs']
print(f"Dependent variable/Target: {y.name}")

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# training
model_le = LinearRegression()
model_le.fit(X_train, y_train)

# prediction
preds_le = model_le.predict(X_test)
print(pd.DataFrame({'Actual': y_test, 'Predicted': np.round(preds_le, 2)}).head())

# evaluation
r2_le = r2_score(y_test, preds_le)
mse_le = mean_squared_error(y_test, preds_le)
print(f"""R² Score: {r2_le:0.6f}, MSE: {mse_le:0.6f}""")
Independent variable/Feature(s): ['size_sqft', 'city_le']
Dependent variable/Target: price_lakhs
     Actual  Predicted
521     108      74.01
737      48      74.04
740     113      74.03
660     112      74.00
411      69      74.18
R² Score: -0.002678, MSE: 671.469921

6.3 Target Enconding

Code 
X = df_te[['city_target', 'size_sqft']]
print(f"Independent variable/Feature(s): {list(X.columns)}")
y = df_te['price_lakhs']
print(f"Dependent variable/Target: {y.name}")

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# training
model_te = LinearRegression()
model_te.fit(X_train, y_train)

# prediction
preds_te = model_te.predict(X_test)
print(pd.DataFrame({'Actual': y_test, 'Predicted': np.round(preds_te, 2)}).head())

# evaluation
r2_te = r2_score(y_test, preds_te)
mse_te = mean_squared_error(y_test, preds_te)
print(f"""R² Score: {r2_te:0.6f}, MSE: {mse_te:0.6f}""")
Independent variable/Feature(s): ['city_target', 'size_sqft']
Dependent variable/Target: price_lakhs
     Actual  Predicted
521     108      75.00
737      48      70.18
740     113      75.04
660     112      76.31
411      69      76.63
R² Score: -0.000205, MSE: 669.813730

6.4 Comparison

Code 
# Compare R² across encoders

results_df = pd.DataFrame({
'Encoding': ['One-Hot', 'Label', 'Target'],
'R2_Score': [r2_ohe, r2_le, r2_te],
'MSE': [mse_ohe, mse_le, mse_te]
})

plt.figure(figsize=(6,4))
plt.bar(results_df['Encoding'], results_df['R2_Score'],
color=['#4CAF50', '#FF9800', '#2196F3'], edgecolor='black')
plt.title('Regression Performance by Encoding Type', fontsize=13)
plt.xlabel('Encoding Method')
plt.ylabel('R² Score')
plt.grid(axis='y', linestyle='--', alpha=0.6)
plt.show()

Code 
plt.figure(figsize=(8, 4))
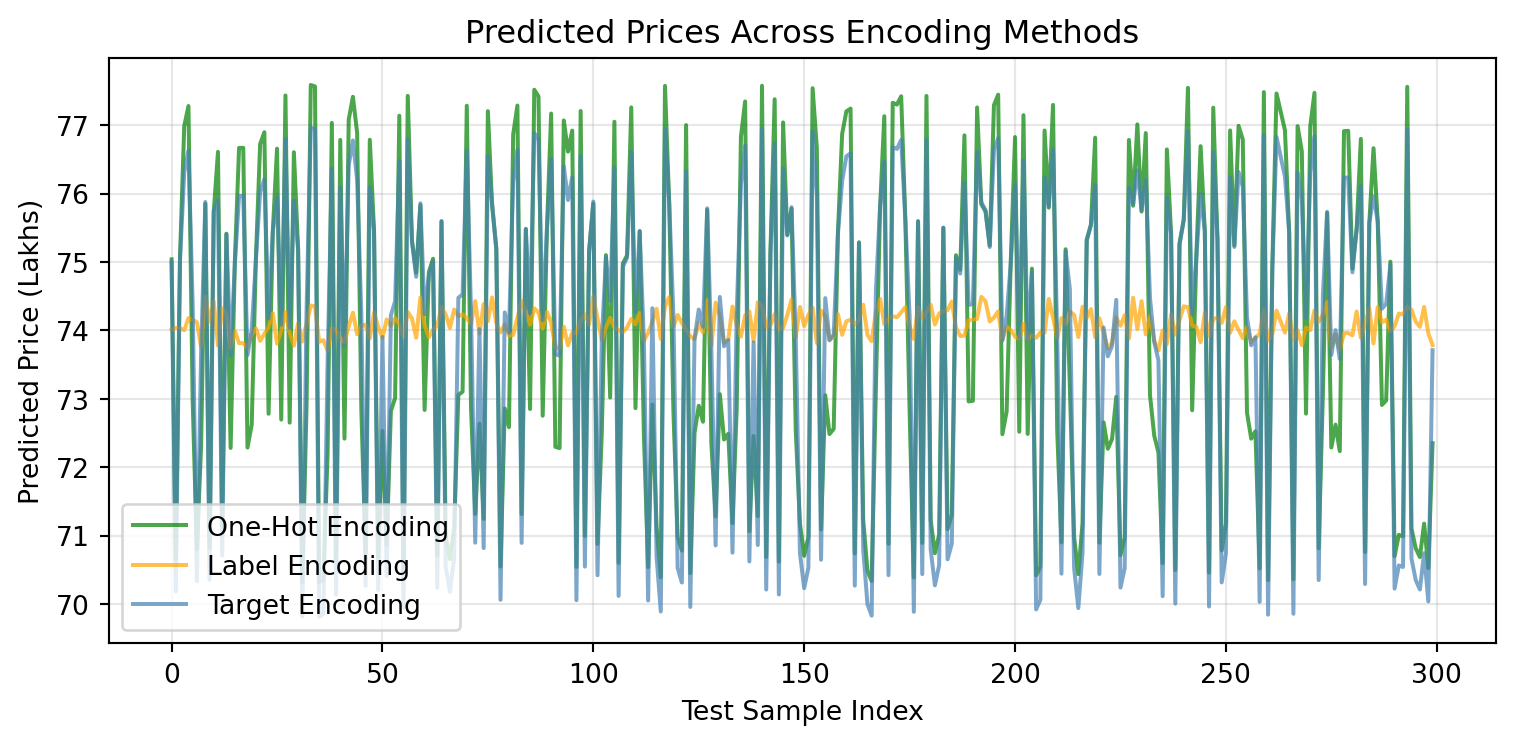
plt.plot(preds_ohe, label='One-Hot Encoding', color='green', alpha=0.7)
plt.plot(preds_le, label='Label Encoding', color='orange', alpha=0.7)
plt.plot(preds_te, label='Target Encoding', color='steelblue', alpha=0.7)

plt.title("Predicted Prices Across Encoding Methods")
plt.xlabel("Test Sample Index")
plt.ylabel("Predicted Price (Lakhs)")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

It shows predicted prices (in lakhs) for test samples indexed from 0 to 300 on the x-axis. The y-axis ranges roughly from 70 to 78 lakhs.

Three different encoding methods are compared:

  • One-Hot Encoding (green line) with high fluctuation in values between about 70 and 77 lakhs.

  • Label Encoding (orange line) which is very stable around 74 lakhs.

  • Target Encoding (blue line) which fluctuates between about 70 and 77 lakhs, somewhat similar to one-hot encoding but with different patterns.

The plot clearly demonstrates how predicted price variance differs depending on the encoding method used for the test samples. Label encoding leads to the most stable price predictions, while one-hot and target encoding lead to more volatile predictions.

7 🧭 Summary

Encoder Type Pros Cons Best For
One-Hot Simple, interpretable High dimensionality Small categorical sets
Label Compact, easy May imply order Tree-based models
Target Handles many categories Risk of leakage Large datasets, regularized models

Categorical encoding isn’t just preprocessing — it’s part of feature engineering intelligence. A good choice of encoding can make or break model performance.

Note

Next time you face a categorical column, remember: “Encoding is not just transformation — it’s translation.”